모두CBT | 국가고시 실기시험 부시기!
2013년 13회 소방수리학·약제화학 및 소방전기 해설 페이지
1번
다음에서 설명하고 있는 열역학 법칙은?
어떤 두 물체 A와 B가 제3의 물체 C와 각각 열평형상태에 있을 때, 두 물체 A와 B도 서로 열평형상태이다.
①열역학 제0법칙
②열역학 제1법칙
③열역학 제2법칙
④열역학 제3법칙
①
제시된 내용은 온도의 존재를 정의하고 측정의 근거를 제공하는 열역학 제0법칙에 대한 설명입니다. A와 C의 온도가 같고, B와 C의 온도가 같다면, A와 B의 온도도 같다는 원리입니다.
2번
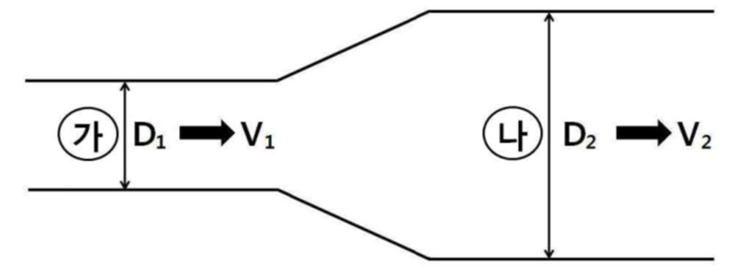
그림과 같은 수평원형배관에 물이 충만하여 흐르는 정상유동에서 가와 나 지점의 유속비 V1/V2 는?(단, 물은 이상유체로 가정하고, 가 지점에서 배관내경은 D1, 물의 유속은 V1이며, 나 지점에서 배관내경은 D2, 물의 유속은 V2라 한다.)
①(D2/D1)^2
②D2/D1
③D1/D2
④(D1/D2)^2
①
유량보존의 법칙(연속의 방정식) Q = A₁V₁ = A₂V₂ 를 적용합니다. 여기서 A는 단면적(πD²/4)입니다. 따라서 (πD₁²/4) * V₁ = (πD₂²/4) * V₂ 이고, 식을 정리하면 D₁²V₁ = D₂²V₂ 입니다. 문제에서 요구하는 유속비 V₁/V₂ = D₂²/D₁² = (D₂/D₁)² 입니다.
3번
물이 수평 원형배관 내를 충만하여 흐를 때 배관 내 어느 한 지점에서 물의 속도가 10 m/s, 물의 정압력이 0.25 MPa일 경우, 물의 속도수두(m)는 약 얼마인가?(단, 중력 가속도는 9.8 m/s² 로 한다.)
①1.1
②3.1
③5.1
④7.1
③
속도수두는 유체의 운동에너지를 높이로 환산한 것으로, 공식은 v² / (2g) 입니다. 여기서 v는 유속(10 m/s), g는 중력가속도(9.8 m/s²)입니다. 속도수두 = 10² / (2 * 9.8) = 100 / 19.6 ≈ 5.1 m 입니다. 문제에 주어진 정압력은 계산에 사용되지 않습니다.
4번
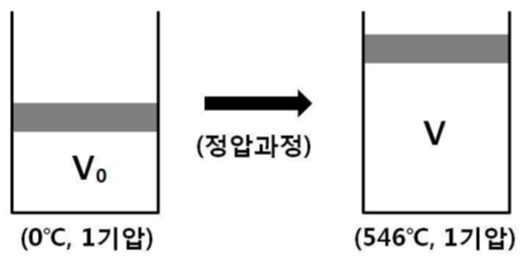
그림과 같이 밀폐계 속에 들어 있는 공기의 압력(1기압)을 일정하게 유지하면서 공기의 온도를 0℃에서 546℃로 증가시켰다. 546℃, 1기압 상태일 때의 공기체적(V)은 0℃, 1기압 상태일 때 공기체적(V₀)의 약 몇 배인가?(단, 공기는 이상기체로 가정한다.)
①2
②3
③4
④5
②
압력이 일정한 조건에서 기체의 부피는 절대온도에 비례한다는 샤를의 법칙(V₁/T₁ = V₂/T₂)을 이용합니다. 절대온도로 변환하면 T₀ = 0℃ + 273 = 273K, T = 546℃ + 273 = 819K 입니다. 따라서 V/V₀ = T/T₀ = 819K / 273K = 3. 즉, 나중 체적(V)은 처음 체적(V₀)의 3배가 됩니다.
5번
관성력과 표면장력의 비를 나타내는 무차원수는?
①그라쇼프(Grashof) 수
②프루드(Froude) 수
③오일러(Euler) 수
④웨버(Weber) 수
④
각 무차원수는 다음과 같은 힘의 비를 나타냅니다. 웨버 수: 관성력/표면장력, 프루드 수: 관성력/중력, 오일러 수: 압력/관성력, 그라쇼프 수: 부력/점성력. 따라서 관성력과 표면장력의 비는 웨버 수입니다.
6번
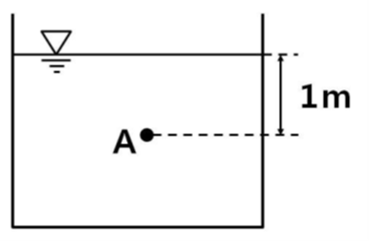
그림과 같이 비중이 1.2인 액체가 대기 중에 상부가 개방된 탱크에 들어 있을 때, A점의 계기압력은 수은주로 약 몇 mmHg인가?(단, 수은의 비중은 13.6, 물의 밀도는 1,000 kg/m³이다.)
①0.9
②16.3
③88.2
④163.2
③
A점의 계기압력 P = γh = (1.2 × 9800 N/m³) × 1m = 11,760 Pa 입니다. 수은주 압력 P_Hg = γ_Hg * h_Hg 이므로, h_Hg = P / γ_Hg = 11,760 / (13.6 × 9800) ≈ 0.0882m 입니다. 이를 mmHg로 환산하면 0.0882m × 1000mm/m = 88.2 mmHg 입니다.
7번
내경이 D, 길이가 L인 직관으로 이루어진 소화배관에서 흐르는 물의 양이 200l/min 일 때 마찰손실압력은 0.02MPa이다. 이 소화배관에서 흐르는 물의 양이 400ℓ/min로 증가한다면 마찰손실압력(MPa)은 약 얼마인가?(단, 마찰손실계산은 Hazen-Williams의 식을 따르고, 소화배관의 조도계수는 일정하다.)
①0.062
②0.072
③0.082
④0.092
②
하젠-윌리엄스 식에서 마찰손실압력(ΔP)은 유량(Q)의 1.85제곱에 비례합니다(ΔP ∝ Q^1.85). 따라서 (ΔP₂/ΔP₁) = (Q₂/Q₁)^1.85 입니다. ΔP₂ = 0.02 * (400/200)^1.85 = 0.02 * 2^1.85 ≈ 0.02 * 3.606 ≈ 0.072 MPa 입니다.
8번
옥내소화전설비에 사용하는 소화펌프의 토출량이 1,000 l/min, 전양정이 100m, 펌프 전효율이 65%일 때 전동기의 출력(kW)은 약 얼마인가?(단, 소화펌프와 전동기의 동력전달계수(K)는 1.1로 가정한다.)
①22.6
②25.6
③27.6
④30.6
③
전동기 출력 공식 P(kW) = (0.163 × Q × H × K) / η 를 사용합니다. 여기서 Q(토출량)=1 m³/min, H(전양정)=100m, K(전달계수)=1.1, η(효율)=0.65 입니다. P = (0.163 * 1 * 100 * 1.1) / 0.65 = 17.93 / 0.65 ≈ 27.6 kW 입니다.
9번
다음 중 화학적 소화원리에 해당하는 것은?
①부촉매소화
②질식소화
③냉각소화
④희석소화
①
소화의 원리는 물리적 소화(냉각, 질식, 제거, 희석)와 화학적 소화(억제, 부촉매)로 나뉩니다. 부촉매(억제)소화는 할로겐화합물 소화약제가 연소의 연쇄반응을 차단하는 원리로, 유일한 화학적 소화 방법입니다.
10번
포소화약제의 유화효과(emulsion effect)를 이용하여 소화할 수 있는 방호대상물로 가장 적합한 장소는?
①전자제품창고
②유류저장고
③종이창고
④귀금속상점
②
유화효과는 포소화약제가 유류 표면에서 기름과 섞여 유화층을 형성하여 유증기 발생을 억제하는 소화 효과입니다. 이 효과는 유류 화재에 특히 유효하므로, 방호대상물로 유류저장고가 가장 적합합니다.
11번
소화수에 사용되는 첨가제 중 침투제에 관한 설명으로 옳은 것은?
①물의 표면장력을 감소시켜 심부화재소화를 돕는 첨가제
②가연물과의 유화층 형성을 돕는 첨가제
③물의 동결을 방지하기 위한 첨가제
④물의 점도를 증가시켜 쉽게 흘러 유실되는 것을 방지하는 첨가제
①
침투제(Wetting Agent)는 계면활성제의 일종으로, 물의 표면장력을 낮추어 물이 목재, 섬유 등 고체 가연물 깊숙이 침투하도록 돕는 역할을 합니다. 이를 통해 심부화재의 냉각소화 효과를 높입니다.
12번
포노즐을 통하여 포수용액 80ℓ를 포팽창비 5.0으로 방출시킬 경우 방출된 포의 체적(l)은?
①0.0625
②16
③80
④400
④
포 팽창비는 (방출된 포의 체적) / (사용한 포 수용액의 체적)으로 정의됩니다. 따라서 방출된 포의 체적 = 포 수용액 체적 × 팽창비 = 80 L × 5.0 = 400 L 입니다.
13번
질식소화를 위한 연소한계산소농도가 14.7 vol%인 가연물질의 소화에 필요한 CO₂ 가스의 최소소화농도(vol%)는?(단, 무유출(No efflux)방식을 전제로 한다.)
①28
②30
③34
④36
②
CO₂의 최소소화농도(C) 계산 공식은 C = (21 - O₂) / 21 * 100 입니다. 여기서 O₂는 연소한계산소농도(14.7%)입니다. C = (21 - 14.7) / 21 * 100 = 6.3 / 21 * 100 = 30% 입니다.
14번
다음 분말소화약제의 열분해 반응식과 관계가 있는 것은?
NH₄H₂PO₄→ NH₃+H₂O+HPO₃-76.95 kcal
①제1종 분말소화약제
②제2종 분말소화약제
③제3종 분말소화약제
④제4종 분말소화약제
③
제시된 반응식의 반응물인 NH₄H₂PO₄는 제1인산암모늄으로, 제3종 분말소화약제의 주성분입니다. 제3종 분말은 열분해 시 생성되는 메타인산(HPO₃)이 가연물 표면에 유리질의 피막을 형성하여 산소 공급을 차단하는 질식 및 방진 효과를 나타내어 A급 화재(심부화재)에도 적응성이 있습니다.
15번
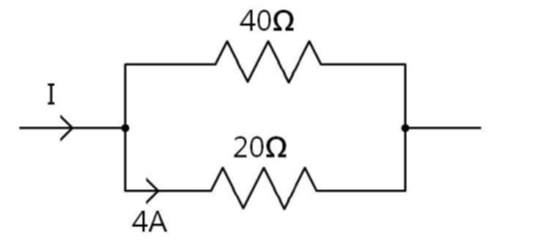
그림과 같은 회로에서 저항 20Ω에 흐르는 전류가 4A라면, 전류 I(A)는?
①6
②8
③10
④12
①
병렬회로에서는 각 저항에 걸리는 전압이 동일합니다. 20Ω 저항에 걸리는 전압 V = I × R = 4A × 20Ω = 80V 입니다. 이 전압은 40Ω 저항에도 동일하게 걸리므로, 40Ω 저항에 흐르는 전류 I' = V / R' = 80V / 40Ω = 2A 입니다. 전체 전류 I는 두 전류의 합이므로, I = 4A + 2A = 6A 입니다.
16번
회로에 100V의 전압을 인가하였더니 5A의 전류가 흘러 72kcal의 열량이 발생하였다. 이때 전류가 흐른 시간(초)은?
①0.6
②6
③60
④600
④
줄의 법칙에 따라 열량 H = 0.24 * P * t (cal) 입니다. 전력 P = V * I = 100V * 5A = 500W 입니다. H = 72kcal = 72,000cal 이므로, t = H / (0.24 * P) = 72,000 / (0.24 * 500) = 72,000 / 120 = 600초 입니다.
17번
정전용량이 같은 콘덴서 2개의 병렬합성 정전용량은 직렬합성 정전용량의 몇 배인가?
①2
②4
③5
④8
②
정전용량을 C라고 할 때, 2개를 병렬로 연결하면 합성 정전용량 C_p = C + C = 2C 입니다. 직렬로 연결하면 1/C_s = 1/C + 1/C = 2/C 이므로, C_s = C/2 입니다. 따라서 병렬합성 정전용량(2C)은 직렬합성 정전용량(C/2)의 4배입니다. (2C) / (C/2) = 4.
18번
100회 감은 코일과 쇄교하는 자속이 0.2초 동안에 5Wb에서 2Wb로 감소할 경우, 코일에 유도되는 기전력(V)은?
①300
②1,000
③1,500
④2,500
③
패러데이의 전자기 유도 법칙에 따라 유도기전력 e = -N * (ΔΦ/Δt) 입니다. 여기서 N(권선수)=100, ΔΦ(자속변화량)=2-5=-3Wb, Δt(시간변화량)=0.2초 입니다. 유도기전력의 크기는 e = | -100 * (-3 / 0.2) | = | -100 * -15 | = 1,500 V 입니다.
19번
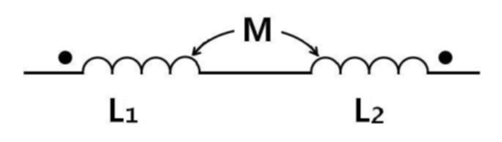
그림과 같이 직렬로 접속된 2개의 코일에 5A의 전류를 흘릴 때 결합된 합성코일에 발생하는 자기 에너지(J)는?(단, 코일의 자기 인덕턴스 L₁=L₂=20mH, 상호인덕턴스 M=10mH이다.)
①0.2
②0.25
③0.3
④0.4
②
코일이 가동결합(같은 방향으로 감김)된 직렬회로의 합성 인덕턴스 L = L₁ + L₂ + 2M 입니다. L = 20mH + 20mH + 2(10mH) = 60mH = 0.06H. 코일에 저장되는 자기 에너지 W = (1/2)LI² = (1/2) * 0.06H * (5A)² = 0.03 * 25 = 0.75J. 만약 차동결합이라면 L = L₁ + L₂ - 2M = 20mH, W = 0.25J. 그림의 점(dot) 표시가 없어 가동/차동을 판단하기 어려우나, 보기와 정답을 고려할 때 차동결합을 의도한 문제로 보입니다. W = 0.25J.
20번
전기계측기와 지시 값의 연결이 옳지 않은 것은?
①가동코일형 계기 - 평균값 지시
②정전형 계기 - 평균값 및 실효값 지시
③열전형 계기 - 평균값 및 실효값 지시
④유도형 계기 - 평균값 지시
④
각 계측기의 지시값은 다음과 같습니다. 가동코일형: 평균값, 정전형/열전형/전류력계형: 실효값, 유도형: 실효값. 따라서 유도형 계기가 평균값을 지시한다는 설명은 옳지 않습니다.
21번
v=50+20√2sin(ωt+20)+10√2sin(3ωt-40)[V]인 비정현파 교류전압의 실효값(V)은 약 얼마인가?
①23.6
②37.4
③45.7
④54.8
④
비정현파의 실효값은 각 성분(직류분, 기본파, 고조파)의 실효값의 제곱의 합의 제곱근입니다. V_rms = √(V_dc² + V_1² + V_3² + ...). 여기서 직류분 실효값=50V, 기본파 실효값=20V(최대값 20√2 / √2), 3고조파 실효값=10V(최대값 10√2 / √2) 입니다. V_rms = √(50² + 20² + 10²) = √(2500 + 400 + 100) = √3000 ≈ 54.8V 입니다.
22번
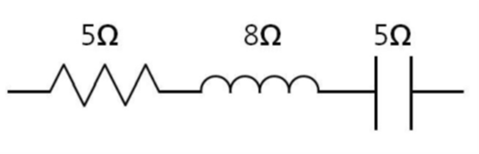
그림과 같이 저항 5Ω, 유도리액턴스 8Ω, 용량리액턴스 5Ω이 직렬로 접속된 회로의 역률은 약 얼마인가?
①0.65
②0.75
③0.86
④0.94
③
역률(cosθ) = 저항(R) / 임피던스(Z) 입니다. 임피던스 Z = √(R² + (X_L - X_C)²) 입니다. Z = √(5² + (8 - 5)²) = √(25 + 3²) = √(25 + 9) = √34 ≈ 5.83Ω. 역률 = 5 / √34 ≈ 0.857 ≈ 0.86 입니다.
23번
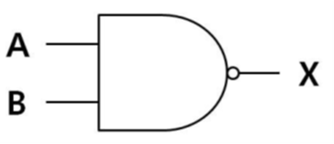
그림과 같은 NAND 게이트와 등가인 논리식은?
①X=A+B
②X=A·B
③X=Ā·B̄
④X=Ā+B̄
④
NAND 게이트의 논리식은 X = (A·B)의 부정(bar) 입니다. 드 모르간의 정리에 따라 (A·B)의 부정은 Ā + B̄ 와 같습니다. 따라서 등가인 논리식은 X = Ā + B̄ 입니다.
24번
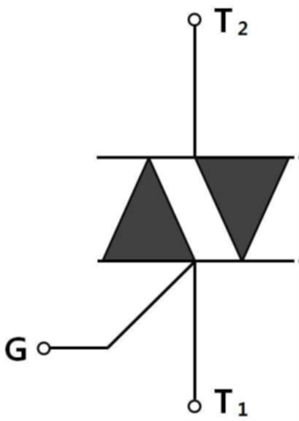
다음 심벌이 의미하는 반도체 소자는?
①DIAC
②TRIAC
③SCR
④SCS
②
그림의 심벌은 2개의 SCR(사이리스터)을 역병렬로 접속한 형태이며, 양방향으로 전류 제어가 가능한 트라이악(TRIAC)을 나타냅니다. 단자 T₁, T₂와 게이트(G)로 구성됩니다.
25번
전선의 표시기호로서 천장은폐배선은?
①실선(─)
②파선(---)
③일점쇄선(-・-)
④이점쇄선(-・・-)
①
전기설비 도면에서 배선 방법의 기호는 다음과 같습니다. 천장은폐배선은 실선(─), 바닥은폐배선은 파선(---), 노출배선은 일점쇄선(-・-)으로 표기합니다.